Kesir sayısı sıfatına nasıl örnek verilebilir?

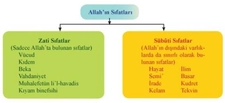
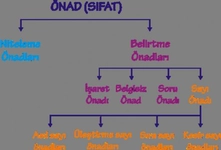
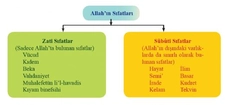
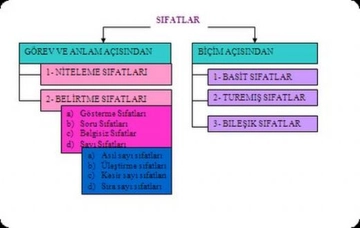
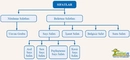
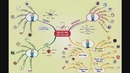
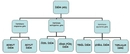
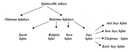
Kesir sayıları, matematiksel işlemler veya günlük yaşamda, bölme işlemini ifade eden sayılardır. Kesirler, bir bütünün parçasını temsil etmek için kullanılır ve genellikle iki sayıdan oluşur: pay (bölünen) ve payda (bölene). Kesir sayılarının sıfatları, bu sayıların niteliğini ve özelliklerini belirten terimlerdir. Aşağıda kesir sayısının sıfatlarına örnekler ve açıklamaları detaylandırılacaktır.

Kesir sayıları için birkaç önemli sıfat türü bulunmaktadır. Bu sıfatlar, kesirlerin matematiksel ve kavramsal analizinde yardımcı olur. Bunlar arasında;

• Basit Kesir
• Kesirli Sayı
• Tam Kesir
• Boş Kesir
• Paydalı Kesir

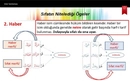
Her bir sıfatın ne anlama geldiği ve örnekleri detaylandırılacaktır.

Basit kesir, payı paydadan küçük olan kesirlerdir. Örneğin; 1/2, 3/4, 5/6 gibi kesirler basit kesirlere örnek verilebilir. Bu tür kesirler, bir bütünün parçalarını ifade eder.

Kesirli sayılar, tam sayı ile bir kesirin birleşimidir. Bu tür sayılar, genellikle bir olayı veya durumu tanımlamak için kullanılır. Örneğin; 2 1/3, 4 3/5 gibi kesirli sayılar, hem tam sayıyı hem de kesiri bir arada barındırır.

Tam kesir, pay ve paydanın birbirine eşit olduğu kesirlerdir. Örnek olarak 4/4, 5/5 gibi kesirler tam kesir olarak adlandırılır. Bu kesirler, bir bütünün tam olarak ifade edildiğini gösterir.

Boş kesir, payın sıfır olduğu kesirlerdir. Örneğin; 0/5, 0/10 gibi kesirler, sıfırın payda dışındaki bütün sayıya bölünmesiyle oluşur. Boş kesir, matematiksel olarak "0" değerini ifade eder.

Paydalı kesir, bir tam sayının bölünemediği durumlarda ortaya çıkar. Örneğin; 1/2, 3/7 gibi kesirler, belirli sayıların tam sayı olarak ifade edilemediği durumlar için kullanılır.

Kesir sayıları, matematikte, bilimde ve günlük hayatta birçok alanda kritik bir öneme sahiptir. Kesirler, özellikle oran, oranlama, ölçme ve bölme işlemlerinde kullanılır. Eğitimde, öğrencilerin kesirlerle ilgili kavramları daha iyi anlamalarını sağlamak amacıyla yaygın bir şekilde öğretilir.

Kesirlerle ilgili bazı temel kavramlar, genellikle öğrencilerin veya insanların bu tür sayıları anlamalarını kolaylaştırmak için açıklanır. Örneğin, kesirlerin karşılaştırılması, toplama ve çıkarma işlemleri gibi temel işlemler eğitim müfredatında önemli bir yere sahiptir. Ayrıca, kesirlerin ondalık kesirlere dönüştürülmesi ve tam sayılara çevrilmesi gibi konular da geniş bir şekilde ele alınmaktadır.

Sonuç olarak, kesir sayıları matematiksel ifadenin önemli bir parçasıdır ve sıfatları, bu sayıların özelliklerini anlamamıza yardımcı olur. Kesirlerin uygulanabilirliği, hem teorik hem de pratik alanlarda geniş bir yelpazeye yayılmaktadır. Kesirlerin öğrenilmesi, bireylerin matematiksel düşünme becerilerini geliştirmelerine katkı sağlar.