
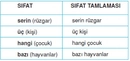
Kesir sayıları için hangi sıfat örnekleri verilebilir?
Kesir sayıları, matematikte bir bütünün parçalarını temsil eder. Bu sayılar, günlük yaşamda ve hesaplamalarda yaygın olarak kullanılır. Kesirlerin sınıflandırılması ve nitelendirilmesi, matematiksel işlemlerin doğruluğunu artırır. Bu yazıda kesirlerin çeşitleri ve özellikleri ele alınacaktır.
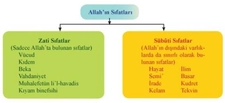
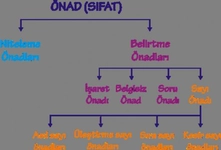
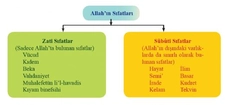
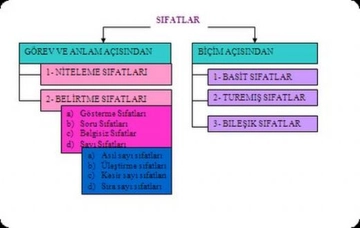
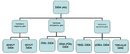
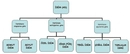
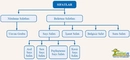
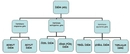
Kesir Sayıları ve Sıfatların Önemi Kesir sayıları, matematikte bir bütünün parçasını temsil eden sayılardır. Bu sayılar, genellikle bir pay (numerator) ve bir payda (denominator) ile ifade edilir. Kesirlerin kullanımı, matematiksel hesaplamalarda ve günlük yaşamda oldukça yaygındır. Kesir sayılarının tanımlanması ve sınıflandırılması sırasında, bu sayılara ait çeşitli sıfatlar kullanılır. Bu makalede, kesir sayıları için kullanılabilecek sıfatlar detaylı bir şekilde ele alınacaktır. Kesir Sayılarının Sınıflandırılması Kesir sayıları, çeşitli kriterlere göre sınıflandırılabilir. Bu sınıflandırma, sıfatların kullanımını doğrudan etkiler. Genel olarak kesir sayıları aşağıdaki gibi gruplandırılabilir:
Bu gruplar, kesirlerin yapılarına ve özelliklerine göre farklı sıfatlarla tanımlanabilir. Kesir Sayıları için Kullanılabilecek Sıfatlar Kesir sayıları için kullanılabilecek bazı sıfatlar aşağıda belirtilmiştir:
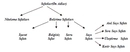
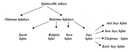
Bu sıfatlar, kesirlerin özelliklerini ve durumlarını açıklamak için önemlidir. Basit Kesirler Basit kesirler, payı paydadan küçük olan kesirlerdir. Örneğin, 1/2, 3/4 gibi kesirler basit kesirlerdir. Bu tür kesirler genellikle "küçük" veya "basit" sıfatlarıyla tanımlanır. Kompleks Kesirler Kompleks kesirler, payı paydadan büyük veya eşit olan kesirlerdir. Örneğin, 5/4 veya 3/3 gibi kesirler. Bu kesirler genellikle "büyüktür" veya "tam" sıfatlarıyla tanımlanabilir. Kesirli Sayılar Kesirli sayılar, bir tam sayı ile bir kesir birleşiminden oluşur. Örneğin, 2 1/2 veya 3 3/4 gibi. Bu tür kesirler "karmaşık" veya "bütün" sıfatlarıyla ifade edilebilir. Kesirlerin Matematiksel Kullanımı Kesir sayıları, matematiksel işlemlerde sıklıkla kullanılır. Özellikle oran, orantı, yüzdelik hesaplamalar ve bölme işlemlerinde önemli yer tutar. Kesirlerin doğru bir şekilde tanımlanması ve sıfatlarla ifade edilmesi, matematiksel işlemlerin doğruluğunu artırır. Sonuç Kesir sayıları, matematikte önemli bir yere sahiptir ve çeşitli sıfatlarla tanımlanabilir. Bu sıfatlar, kesirlerin özelliklerini ve durumlarını daha iyi anlamamıza yardımcı olur. Kesirlerin doğru bir şekilde sınıflandırılması ve sıfatlarla tanımlanması, hem matematiksel işlemlerde hem de günlük yaşamda kesirlerin etkin bir şekilde kullanılmasını sağlar. Ek Bilgiler Kesir sayıları ile ilgili daha fazla bilgi edinmek için matematik kitapları, online kaynaklar ve eğitim platformlarından yararlanabilirsiniz. Ayrıca, kesirlerin grafiksel temsili, kesirler arası dönüşüm ve kesirli sayıların toplama, çıkarma, çarpma ve bölme işlemleri üzerinde durulması gereken önemli konulardır. |




























Kesir sayılarının önemi hakkında düşündüğümde, günlük yaşamda ne kadar sık karşılaştığımızı fark ediyorum. Özellikle yemek tariflerinde veya finansal hesaplamalarda kesirler gerçekten hayatımızı kolaylaştırıyor. Basit kesirlerin tanımının yanı sıra, kompleks kesirlerin nasıl kullanıldığı da merakımı cezbetti. Bu bağlamda, kesirli sayıların nasıl oluştuğu ve nasıl ifade edildiği de beni düşündürüyor. Matematiksel işlemlerde bu kesirlerin doğru bir şekilde tanımlanması ve sınıflandırılması, gerçekten de işlemlerin doğruluğu açısından ne kadar kritik bir öneme sahip! Kesirlerin çeşitli sıfatlarla ifade edilmesi, onların özelliklerini anlamamıza nasıl yardımcı oluyor? Bu konudaki görüşlerinizi merak ediyorum.
Kesirlerin sıfatlarla ifade edilmesi konusundaki düşüncelerini paylaştığın için teşekkürler Duysal Bey. Haklısınız, kesirler günlük hayatın vazgeçilmez bir parçası ve doğru anlaşılmaları büyük önem taşıyor.
Kesirlerin Sıfatlarla İfadesinin Önemi
Kesirleri "basit", "bileşik", "tam sayılı" veya "ondalık" gibi sıfatlarla tanımlamak, öncelikle onların yapısal özelliklerini anlamamızı sağlar. Örneğin, bir kesrin "basit" olarak adlandırılması, payının paydasından küçük olduğunu ve bir bütünden parça ifade ettiğini anında anlamamıza yardımcı olur.
İşlem Kolaylığı
Sıfatlandırma, matematiksel işlemleri doğru yapmamızı sağlar. Bileşik kesri tam sayılı kesre çevirmek, bölme işlemlerinde daha anlamlı sonuçlar vermemize olanak tanır. Aynı şekilde, ondalık kesirlerin günlük hayatta (finans veya ölçümlerde) daha pratik kullanılması da bu sınıflandırmanın avantajıdır.
Kavramsal Anlama
Kesir türlerini sıfatlarla ayırt etmek, matematiksel dilde netlik sağlar. "Kompleks kesir" gibi terimler, iç içe geçmiş oranları anlamamıza ve bunları sadeleştirme yöntemlerini uygulamamıza rehberlik eder.
Sonuç olarak, kesirlerin sıfatlarla ifade edilmesi, hem pratik uygulamalarda hem de teorik anlayışta bize yol gösteren bir araçtır. Bu sınıflandırmalar olmasaydı, kesirlerle çalışmak çok daha karmaşık bir hal alırdı.