Asıl sayıları hangi sıfatlarla örneklendirebiliriz?

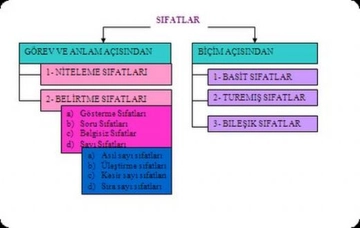
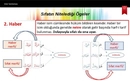
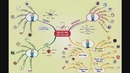
Asıl Sayılar: Tanım ve Özellikleri

Asıl sayılar, doğal sayılar arasında yer alan ve yalnızca 1 ve kendisi olmak üzere iki pozitif böleni bulunan sayılardır. Matematikte önemli bir yer tutan asıl sayılar, birçok teorinin temel taşlarını oluşturur. Bu yazıda, asıl sayıların özelliklerini ve bu özellikleri hangi sıfatlarla örneklendirebileceğimizi inceledik.

Asıl Sayıların Temel Özellikleri

Asıl sayılar, bazı belirgin özelliklere sahiptir. Bu özellikler, matematiksel anlamda bu sayıların nasıl sınıflandırıldığını ve kullanıldığını anlamamıza yardımcı olur.

• Pozitif Tam Sayılar: Asıl sayılar, yalnızca pozitif tam sayılar arasında bulunur. Bu, asıl sayıların negatif veya sıfır olamayacağı anlamına gelir.
• Bölünebilirlik: Asıl sayılar, yalnızca 1 ve kendileri haricinde başka bir sayıya tam bölünemezler. Bu, onların benzersizliğini simgeler.
• Sonsuzluk Özelliği: Asıl sayıların sayısı sonsuzdur. Yani, her zaman yeni asıl sayılar keşfedilebilir.
• Asıl Sayılar Arasındaki Farklar: Asıl sayılar, iki ardışık asıl sayı arasında daima en az bir veya daha fazla bileşik sayı bulunduran bir yapıya sahiptir.

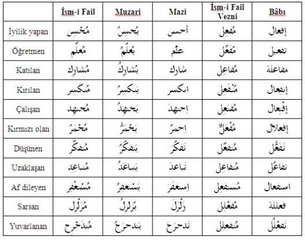
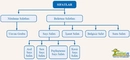
Asıl Sayılar ve Matematiksel Kavramlar

Asıl sayılar, birçok matematiksel kavramın temelini oluşturur. Bu kavramlar, asıl sayıların analizi ve uygulanması açısından büyük önem taşır.

• Asal Çarpanlar: Herhangi bir pozitif tam sayı, bir veya daha fazla asıl sayının çarpanları olarak ifade edilebilir. Örneğin, 28 sayısı 2 x 2 x 7 olarak asal çarpanlarına ayrılır.
• Asal Sayı Teorisi: Bu, asıl sayıların dağılımı ve özellikleri hakkında derinlemesine tartışmalar içeren bir matematik dalıdır. Aritmetik ve sayı teorisi açısından büyük önem taşır.
• Kriptografi: Modern bilgi güvenliği ve kriptografide, asal sayılar önemli bir yer tutar. Güçlü bir şifreleme için genellikle büyük asal sayılar kullanılır.

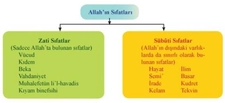
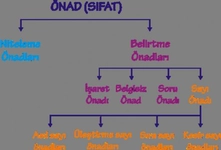
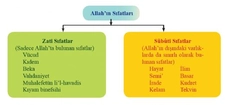
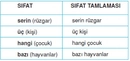
Asıl Sayıların Örnekleri ve Sıfatları

Asıl sayılar, belirli sıfatlarla nitelendirilebilir. İşte bazı önemli örnekler:

• Küçük Asal Sayılar: 2, 3, 5, 7 gibi ilk birkaç asıl sayı oldukça bilinen örneklerdir.
• Büyük Asal Sayılar: 97, 101, 103 gibi daha büyük asıl sayılar, özellikle sayı teorisindeki araştırmalarda önemli bir yer tutar.
• Çift ve Tek Asal Sayılar: 2 asıl sayısı tek olan tek çift asal sayıdır; diğer tüm asıl sayılar ise tektir.

Asıl Sayıların Günlük Hayattaki Yeri

Asıl sayılar, yalnızca matematiksel disiplin içinde değil, aynı zamanda günlük yaşamda da karşılaşabileceğimiz önemli unsurlardır.

• Oyunlar ve Bulmacalar: Birçok bulmacada ve strateji oyunlarında asıl sayılar kullanılmaktadır.
• Müzik Teorisi: Müzik notaları arasında asıl sayıların belirli bir rolü vardır, örneğin, armonik yapılar ve akorlar arasında asıl sayılar temel olarak yer alır.
• Doğa ve Bilim: Asıl sayılar, doğada ve bilim alanında düzenleri ve örüntüleri açıklamak için de kullanılır.

Sonuç

Asıl sayılar, matematiğin en önemli bileşenlerinden biridir ve çeşitli sıfatlarla nitelendirilebilirler. Bu sayılar, yalnızca matematiksel kavramlarda değil, günlük yaşamda da karşımıza çıkmakta ve çeşitli alanlarda önemli roller oynamaktadır. Asıl sayıların daha iyi anlaşılması, matematiksel düşüncenin gelişimine katkı sağlamakta ve çeşitli bilimsel alanlarda uygulamalara zemin hazırlamaktadır.