
Üleştirme Sayısı Nedir Ve Nasıl Tanımlanır?
Üleştime sayısı, belirli bir kümedeki elemanların kombinasyonlarını analiz eden matematiksel bir terimdir. Kombinasyon hesaplamalarında sıkça kullanılan bu kavram, istatistik ve mühendislik gibi pek çok alanda önemli bir yere sahiptir.
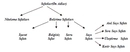
Üleştime Sayısı Nedir Ve Nasıl Tanımlanır?Üleştime sayısı, matematiksel bir kavram olup, belirli bir küme içerisindeki elemanların birbirleriyle olan ilişkilerini ifade eder. Genellikle kombinatorik matematikte, bir nesne kümesinin alt kümelerinin sayısal değerini belirlemek için kullanılır. Üleştime sayısı, belirli bir düzen veya yapı içerisindeki öğelerin nasıl bir araya getirileceğini analiz etmeye yardımcı olur. Bu kavram, özellikle olasılık teorisi, istatistik ve çeşitli mühendislik alanlarında yaygın olarak uygulanmaktadır. Üleştime Sayısının Matematiksel Tanımı Üleştime sayısı, genellikle "n" nesnenin "r" nesne ile bir araya getirilmesi durumunda "n" nesne içerisinde "r" nesne seçme yollarının sayısını ifade eder. Bu durum, aşağıdaki formülle gösterilir:
Burada "n!" ifadesi, "n" faktöriyelini temsil eder ve "r" ise seçilecek eleman sayısını belirtir. Üleştime Sayısının Örnekleri Üleştime sayısının daha iyi anlaşılabilmesi için bazı örnekler üzerinden açıklama yapmak faydalı olacaktır:
Üleştime Sayısının Uygulama Alanları Üleştime sayısı, çeşitli alanlarda önemli bir yere sahiptir. Başlıca uygulama alanları şunlardır:
Sonuç Üleştime sayısı, matematiksel ve pratik açıdan son derece önemli bir kavramdır. Farklı alanlarda, özellikle kombinatorik analiz ve olasılık hesaplamalarında sıkça başvurulan bir yöntemdir. Elemanların bir araya getirilmesi, seçim süreçleri ve veri analizi gibi uygulamalarıyla, günümüz bilim ve mühendislik disiplinlerinde vazgeçilmez bir araç olarak yer almaktadır. Bu makale, üleştime sayısının tanımını, matematiksel formülünü ve uygulama alanlarını açıklamaktadır. Gelişen teknolojiler ve matematiksel yöntemlerle birlikte, üleştime sayısının önemi ve kullanımı artmaya devam etmektedir. |




























Üleştime sayısı hakkında bahsettiğiniz kavramlar gerçekten ilginç. Özellikle kombinatorik matematikteki yeri ve olasılık teorisi ile bağlantısı dikkat çekici. Bir sınıfta belirli sayıda öğrenciden nasıl seçim yapıldığını düşünmek, günlük hayatta sıkça karşılaşılan bir durum. Örneğin, 5 öğrenciden 2'sini seçmek gerektiğinde çıkan farklı kombinasyon sayısını bilmek, öğretmenler için oldukça faydalı bir bilgi olabilir. Ayrıca, finansal kararlar alırken alternatiflerin değerlendirilmesinde bu tür hesaplamaların önemli olduğunu düşünüyorum. Peki, bu tür hesaplamaları yaparken karşılaştığınız zorluklar neler oldu? Uygulama alanları arasında mühendislik ve istatistik gibi pek çok farklı disiplin varken, sizin için en ilginç olan hangi alan?
Değerli Oğuzalp,
Yorumunuzda belirttiğiniz kombinatorik matematik ve olasılık teorisinin günlük hayatta nasıl yer bulduğu gerçekten etkileyici. Özellikle sınıflarda öğrenci seçimi gibi pratik durumlar, bu teorilerin ne kadar kullanışlı olduğunu gösteriyor.
Kombinasyon Hesaplamalarının Zorlukları
Bu tür hesaplamalar yaparken karşılaşılan zorluklar genellikle karmaşıklık ve zaman yönetimi ile ilgilidir. Özellikle büyük gruplar için seçim yaparken, kombinasyon sayıları hızla artar ve bu da hesaplamaları zorlaştırır. Ayrıca, yanlış hesaplamalar sonucunda elde edilen sonuçların güvenilirliğini sağlamak da ayrı bir zorluk.
İlginç Uygulama Alanları
Uygulama alanları arasında mühendislik ve istatistik gibi pek çok farklı disiplin bulunması, bu hesaplamaların geniş bir yelpazede kullanıldığını gösteriyor. Kişisel olarak, istatistik alanındaki uygulamalar benim için daha ilginç. Veri analizi ve sonuçların yorumlanması, karar verme süreçlerinde büyük bir öneme sahip. Özellikle veri bilimi ve makine öğrenimi gibi alanlarda, kombinatorik yaklaşımlar oldukça etkili sonuçlar doğurabiliyor.
Bu konular üzerine düşünmek ve tartışmak oldukça keyifli. Umarım gelecekte bu tür hesaplamalarla ilgili daha fazla örnek ve deneyim paylaşabiliriz.
Saygılarımla,