Kesir sayısı sıfatlarına hangi örnekler verilebilir?

Kesir sayıları, bir bütünün belli bir parçasını ifade eden sayılardır. Genellikle, pay ve payda olmak üzere iki ana bileşenden oluşurlar. Kesir sayılarının sıfatları, belirli bir kesir sayısını nitelendiren ve ona özellik katan terimlerdir. Bu makalede, kesir sayısına ait sıfatların tanımları ve örnekleri üzerinde durulacaktır.

Kesir, a/b biçiminde yazılır; burada 'a' pay, 'b' ise paydadır. Pay, kesirin kaç birim alındığını gösterirken, payda ise toplam birim sayısını belirtir. Örneğin, 3/4 kesiri, bir bütünden 4 birim alınmışsa bu bütünün 3 birimlik kısmını ifade eder.

Kesir sayıları, genellikle bazı sıfatlar ile nitelendirilir ve bu sıfatlar kesirin özelliklerini daha net bir biçimde ifade etmeye yarar. İşte kesir sayılarında kullanılabilecek bazı sıfat türleri:

• Tam Kesir: Payı, paydasına eşit ya da daha büyük olan kesirlerdir. Örneğin, 5/5 veya 7/4.
• Basit Kesir: Payı, paydasından küçük olan kesirlerdir. Örneğin, 1/3 veya 2/5.
• Bileşik Kesir: Payı, paydasından büyük veya eşit olan kesirlerdir. Örneğin, 9/4 veya 8/8.
• Negatif Kesir: Negatif bir sayıyı ifade eden kesirlerdir. Örneğin, -2/3 veya -5/7.
• Pozitif Kesir: Pozitif bir sayıyı ifade eden kesirlerdir. Örneğin, 1/2 veya 3/5.
• Bire Bir Kesir: Payı ve paydası eşit olan kesirlerdir; bu kesirlerin sonucu 1 olur. Örneğin, 3/3 veya 8/8.

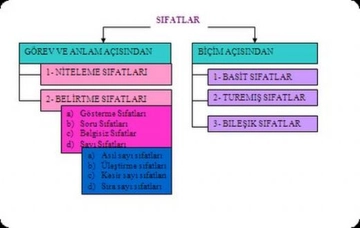
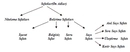
Kesir sıfatları, matematiksel problemlerde olduğu kadar günlük hayatta da sıkça kullanılmaktadır. Örneğin, yemek tariflerinde, malzeme ölçülerinde veya günlük alışverişlerde kesir sıfatları ile dikkatlice ölçüm yapmak gerekir. Bu sıfatlar, yemek yaparken veya mühendislikte hesaplamalar yaparken de önemli bir rol oynar.

Kesirler, birbirinden farklı şekillerde sınıflandırılabilir. Bunu hem matematiksel kurallara hem de pratik yaşantıya göre ele almak mümkündür.

• Dört Temel İşlem: Kesirlerle toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir. Bu işlemlerin kuralları farklı kesir türlerine göre değişkenlik gösterir.
• Orantı ve Oran: Kesirler, oranlar ve orantılar kurmak için kullanılır. Bu da farklı bilim dallarında büyük öneme sahiptir.
• Karmaşık Kesirler: Karmaşık sayıları ifade etmek için kesirler sıklıkla kullanılır. Bu bağlamda, kesirlerin sıfatları ve türleri daha da önem kazanır.

Kesir sayıları, hem eğitim hem de pratik yaşamda önemli bir alana sahiptir. Kesir sıfatlarının doğru bir şekilde tanınması ve anlaşılması, problemlerin çözümlenmesine ve matematiksel düşünme becerilerinin gelişmesine katkı sağlar. Bu nedenle, kesir sayılarının ve sıfatlarının öğrenilmesi, bireylerin matematiksel yeterliliklerini artırmak için büyük bir fırsattır.

Kesir sayılarının eğitimi, özellikle ilkokul ve ortaokul düzeyinde büyük önem taşır. Öğrencilere kesir kavramını öğretirken somut nesneler kullanmak, daha iyi kavramalarına yardımcı olur. Ayrıca, kesirlerin grafiksel gösterimleri ile de öğrencilerin kavramsal anlayışları güçlendirilebilir.

Bu noktada, kesir sayıları ve sıfatları konusunda bir derleme yapmış bulunmaktayız. Kesirlerin anlaşılması ve kullanılması, matematiksel düşünme becerilerini geliştirmek için kritik bir rol oynamaktadır. Kesir ile ilgili daha derinlemesine bilgi ve uygulamalar, özellikle ilerleyen eğitim süreçlerinde daha fazla önem kazanacaktır.